Refer Again to the Data From the Mba New Matriculants Survey From Exercise 52:
MBA New-Matriculants Survey. Refer again to the data from the MBA new matriculants survey in exercise 52 .a. Given that a person applied to more than than one school, what is the probability that the person is $24-26$ years old?b. Given that a person is in the 36 -and-over age group, what is the probability that the person practical to more than than 1 school?c. What is the probability that a person is $24-26$ years old or applied to more than one school?d. Suppose a person is known to accept applied to onl
MBA New-Matriculants Survey. Refer again to the data from the MBA new matriculants survey in exercise 52 . a. Given that a person applied to more than i school, what is the probability that the person is $24-26$ years onetime? b. Given that a person is in the 36 -and-over age group, what is the probability that the person practical to more than than 1 school? c. What is the probability that a person is $24-26$ years erstwhile or applied to more than one school? d. Suppose a person is known to have applied to simply ane school. What is the probability that the person is 31 or more years old? e. Is the number of schools applied to independent of age? Explicate.
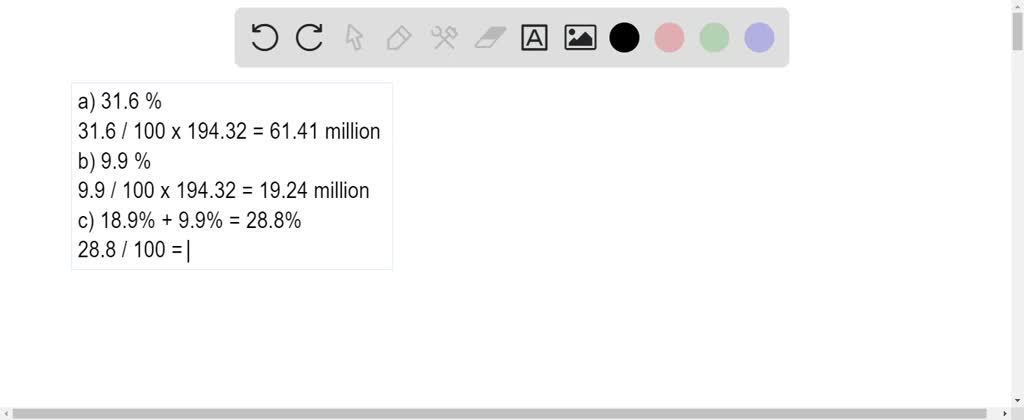
The
educational
attainment of
the
United
States
population
age $ 25 $ years
or
older
in $ 2007 $
is
shown
in
the
circumvolve
graph.
Employ
the
fact
that
the
population
of
people $ 25 $ years
or
older
was approximately $ 194.32 $ million
in $ 2007 $.(a)
Estimate
the
number
of
people $ 25 $ years
or
older who
have
high
schoolhouse
diplomas.(b)
Estimate
the
number
of
people $ 25 $ years
or
older who
have
avant-garde
degrees.(c)
Find
the
probability
that
a
person $ 25 $ years
or
older
selected
at
random
has
earned
a
Bachelors
degree
or
higher.(d)
Find
the
probability
that
a
person $ 25 $ years
or
older selected
at
random
has
earned
a
loftier
schoolhouse
diploma or
gone
on
to
post-secondary
instruction.(e)
Find
the
probability
that
a
person $ 25 $ years
or
older selected
at
random
has
earned
an
Associates
degree or
college.
For this problem. We're told that two% of 2 million loftier schoolhouse students would take the Due south A T every year, requires special accommodations and and then were asked to consider a random sample of 25 students who have recently taken the examination. And nosotros're asking probabilities and then weakened we tin can define Ten as the number of successes existence the number of students who required special adaptation and because we're sampling without replacement from the population. The samples are not strictly independent, but because 25 is far less than 5% of the full population, X tin be pretty reliably estimated every bit a binomial random variable based on 25 size of 25 and the probability of success of 0.ii function A were asked, What is the probability that exactly one required special accommodation? What is the probability that nosotros have exactly one success? So that's the probability mass function for the binomial, and this comes out to approximately zero point 308 now for B were asked, what is the probability that at to the lowest degree 1 received special adaptation? And then what is the probability that nosotros have at to the lowest degree one success nosotros tin can rewrite this as one minus the probability of getting exactly nix successes, and this comes out to approximately naught betoken 397 or C. We're looking for the probability of at least two successes, so this could be rewritten as one minus probability. That Ten is less than or equal to i, and this equals i minus 0.911 which equals 0.89 for a party, you were asked, what is the probability that the number of successes is within two standard deviations of the hateful number of successes or the expected number of successes? Then to calculate this, nosotros must calculate the mean number of successes where this distribution and the standard departure And then for a binomial random variable, the mean or expected value for the number of successes is he going to finish terms? P, which comes out to you 1/2 and the standard deviation of a binomial random variable is given by the square root of N times. P Times Q, which comes out to 0.7, so within two standard deviations of the expected value. We're within this range, and then the mean value is 0.5 and and then plus or minus ii times 0.7, which is the standard divergence, and that gives us a range from minus 0.ix to 1.ix. So that means we're looking for the probability of a certain number of successes. So we for outcomes we can only have integer numbers of students, and that tin't be negative. And so this would exist replaced by zero Tin can't be any lesson nil, and the number two would be more than two standard deviations greater than the expected number. So therefore, nosotros must await for outcomes that are less than or equal to one. So we're looking for the probability that the number of successes is between zero and one, which is the same every bit saying we're looking for the probability of at most i success, which comes out to 0.911 and finally for party. It'due south explained to us that students who receive special adaptation are immune 4.5 hours for the S A T, and students who practise not are allowed iii hours to charge per unit the S A T. And then nosotros're asked, what exercise we expect? The average time allowed for the 25 students to exist, so we tin begin by writing a role that defines the average fourth dimension spent past the 25 students. Then for a student who is given special accommodation to get 4.5 hours, and then we accept 4.5 hours times number of students who get the special accommodation and then the students who don't become iii hours and the number of them volition be 25 minus the number of successes. And to brand it an boilerplate, nosotros must dissever by the number of students, divide by 25. And so this function defines the average number of hours that the students are given for the South A. T out of a sample of 25 and this tin can be simplified as 75 plus one.5 x over 25. So for the question, nosotros're asked, what is the number of hours allocated to the students on average, that nosotros expect. So what is their expected number for the average number of hours allocated to the students? And so what is asking for us? The expected value of the function h of 10. So we can say that is equal to the expected value of 75 plus 1.5 x over 25. And because of the linearity of expectation, we tin can factory with the ane/25 and rewrite the rest of it like this. Now we have 1/25 and then the expected value of a abiding is just that constant. And then nosotros accept 75 plus 1.5 times the expected value for X. And we've already calculated that previously, as 0.five. So this comes out to 3.3 So are we look that the average number of hours allocated to the students to the 25 students writing S A T will exist 3.3 hours.
All right, this question asks us about a binomial experiment with 15 trials and a probability of success of 150.28 So part eh asks for the probability that in that location exactly iv successes and that just plugging into the binomial distribution formula y'all get 15. Choose for times 0.28 to the number of successes times probability of failure to the remaining number of trials, which is the same thing as maxim, If y'all accept a T 84 by a no meal, pdf pdf considering we're only interested in one probability fifteen trials 0.28 success rate and we're interested in 10 equals four. And both of those answers work out 2.2261 All right, And then Function B asks for the probability the X is greater than or equal to three, which equals i minus the probabilities. We don't want soapy zero plus p i plus p too, which tin can be written as one minus the key mood of probability. And then Bynum CDF 15 trials 150.28 probably of success, and we're adding all the probabilities upto X equals 2, and that works out to 0.835 5
In this problem, the table listed the top is the table given in the trouble. Heart asks y'all to find the articulation probabilities for each office. Well, articulation probabilities for the probabilities of each of the numbers in the tabular array. You talk similar these, you lot have those numbers. So, for case, the joint probability between school quality and total time yous calculate that taking the 421 and dividing it by the total number of people, which is 1929 as shown in the bottom right manus corner. This is y'all. A joint probability a 0.2182 Yeah, You practice this for each of the numbers in the tabular array. And then for school price, you would do 393 divided i by 1929 so on and then forth. That gives you the joint probabilities in the middle. And the marginal probabilities are the probabilities of the columns. So for schoolhouse quality, information technology'due south 821 divided by 1929 giving a marginal probability of 19290.4 to 56 for school cost is 986 divided by 1929. To give you a marginal probability of 19290.5111 you do the same thing for full time and part time. Herbie asks what the near important factor for choosing a school appears to be. The three factors were school quality, school cost, slash, convenience and other as seen by the marginal probabilities. School cost has the highest marginal probability, with a probability of 0.5111 Therefore, the most of import gene for choosing a schoolhouse appears to be the school costs are convenience. The next highest was school quality, with a marginal probability of 0.iv to 56 Therefore, the guild for the most important factors were choosing a school appears to be school cost slash convenience offset, followed by school quality, followed past other heart. See asked if a student goes full time, what is the probability this school quality is the starting time reason for choosing a school? This problem is asking you lot to calculate the probability of school quality, given that the student is full time. This is calculated with the articulation probability of quality in full fourth dimension, divided by the probability of being a full fourth dimension student. It'south their iv.2182 divided by the marginal probability of total time, which is 0.4614 to give the probability of a pupil. Choosing quality is the first reason for choosing a school given those student is a total fourth dimension pupil. As 0.47 to 9 political party asked if a student goes function fourth dimension was the probability that schoolhouse quality is the starting time reason for choosing a school. This is the probability of choosing school quality, given that the student is part time. This is calculated by taking the joint probability of quality and function fourth dimension divided past the marginal probability of part time. This is signal to 074 divided past 740.5386 giving a probability of 0.3851 Hurt Due east says. Allow a announce the issue. The commune is full time and be the result. The student list school quality as the showtime reason for utilise. Are the 2 events independent to be contained? The probability of one event cannot depend on the other. However, the probability of a pupil choosing school quality is the outset reason for applying is dependent on whether the educatee is hard time or total time, as shown by the differences in probability in parts See indeed, therefore, events A and B are not independence.
All right, were given some data about graduates and there salaries ten years later graduation, and nosotros've divided them into data for men and data from women. And so for part A, given the statistics Ah, we're given a sample of forty men, and we want to find the probability that our sample hateful will be within 10,000 of our population. Means hold on. Gonna scissure that notation. There we keep that might need his penmanship, only you get the full general idea, right? So let's discover our standard departure of the sampling distribution. It's gonna be the standard difference over sample size. So that's gonna be, uh, twoscore,000 divided by the square root of 40. That equals 6324 56 We're gonna find a Z lower and see upper like so. So for a C lower, uh, it'south gonna be negative. 10,000 divided by our heart difference, uh, for the sample. Yes, our sampling distribution, and so for upper, it'south gonna exist 10,000 positive. When you compute these out, you get negative 1.58 from 1.58 Comparing this to our normal probabilities table. This gives you probability. Lower 0.571 probability, upper 0.9429 Uh, this means our probability is gonna be probability upper minus probability, lower. Which is zippo point 8858 Correct party. Uh, this time nosotros're looking at a sample of 40 women, and now we need to find the probability that our sample mean that we find is inside 10,000 of the mean for the women. So over again, we're going to find our standard deviation sampling distribution. That's gonna be this time. We're looking at the statistics for the women. And then this is going to exist 25,000 over square root of 40. Calculate that out. That's 3952.47 are Sorry. 847 Anyway, allow's notice a Z lowers the upper. So the els you again. That'southward gonna be negative. ten,000 over our standard deviation of the sampling distribution for women. This ane's gonna be 10,000 positive. So these are equal negative. 2.53 two.53 respectively. This is P. L. Looking at our table In one case over again, this lower probability is from zero point 0057 Upper probability 0.9943 Finding a probability, which is probability Oper minus probability, lower. Yous get, um, zero point 9886 office C due south us two compared these to given caption why 1 is higher than the other. And we meet that part. He is greater. This is because standard deviation for men is greater and then that for women I'g gonna take to movement that up on. And considering the standard difference is greater, this means that this is a small This is smaller relative to our standard deviation, which means this allow fewer standard deviations away from the mean, equally opposed to this. All correct, I'1000 gonna motility to a dissimilar page party. Now nosotros have sample of 100 men. We desire to find the probability that air sample mean is within. Ah, I believe information technology is sad. Information technology'southward not within this fourth dimension. We need to observe a sample mean that is greater than our population hateful minus 4000. All correct, so permit'south find our sampling distribution. Ah, standard difference. Then that'southward referring dorsum to hear. That's xl,000 square root of 100 square. 100 is tense. And this only 4000. All right, now we just see score for 4000 against 4000. So this could be because we are looking at 4000 less than the mean That's gonna be negative. 4000 meridian standard deviation is 4000. And then this is negative 1.0 And if we await at our tabular array, this corresponds to a probability is goose egg bespeak 1587 and there yous have it.
Refer Again to the Data From the Mba New Matriculants Survey From Exercise 52:
Source: https://itprospt.com/num/10118604/mba-new-matriculants-survey-refer-again-to-the-data-from